Models are everywhere in modern society. This is far beyond billboards advertising products and in plastic dioramas showing miniaturized versions of cars and trains. Models are used for estimating how much you should pay for automobile insurance to things like the odds of rain. They are simple to complex equations that use variables (numbers that change in response) and parameters (constants or numbers that do not change) to estimate what is going to happen. For example, to precipitation estimating models use variables like the barometric pressure and humidity to make the best guess possible on the unknown amount of rain.

For many natural systems of interest, scientists can tune a model by running an experiment to test if the model accurately predicts the final results. But what about problems or questions where we can’t test the model because of the time or spatial scale involved? Or what about problems where there are unknown numbers of variables and parameters? This is the tough part about modeling natural systems, especially the Critical Zone; think of all the dozens of interactions among water, animals, heat, rock, chemistry together! So how do we model the Critical Zone?

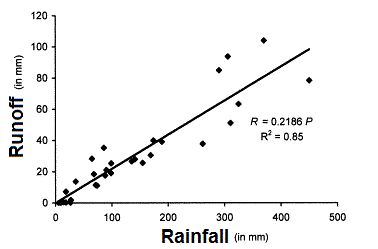
There are many types of number-based models but there are generally two main types used to explore the Critical Zone: empirical models that use known relationships in past events to predict the future and processed-based models that explore how a natural process works but doesn’t necessarily require past events. Empirical models are built using known data and can be used to predict things like carbon dixoide emissions from soils, rain and snowfall, and flooding. One of the classic empirical models is the rainfall-runoff relationship. In this relationship, the amount of runoff can be predicted with a good degree of confidence as shown in Figure 1 in a watershed in Central Himalya, India. This is important for determining if a storm will cause flooding due to increased streamflow from high runoff. However, this is not a perfectly fit line because unknown variables like the amount of water already stored in the soil are not taken into account.

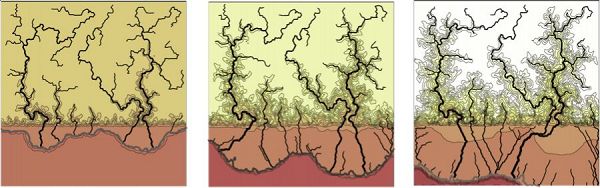
Critical Zone scientists have created many process-based models to tackle big questions like carbon dynamics and landscape evolution. For example, Anthony Parolari et al. (2017) at used a process based model to look at the storage of carbon in trees and belowground during forest regeneration at Calhoun CZO. They found that carbon has non-linear behavior and that relatively simple variables and parameters are needed to accurately explain carbon storage in trees and in the soil below. The Channel-Hillslope Integrated Landscape Development (CHILD) model by Greg Tucker at al (2001) and others is a process-based model that calculates the evolution of hills and soils and in response to streams and other geomorphic actions. This complex model uses variables such as grain size of particles, types of bedrock, and soil creep to look at how landforms develop. Models like CHILD are powerful tools to evaluate Critical Zone processes that occur over such large time intervals and spaces that we cannot conduct an experiment or make enough long-term observations to create empirical models.

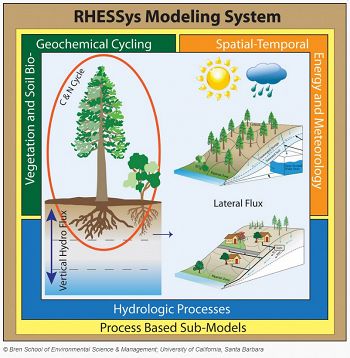
In addition,  Critical Zone scientists have even more complex models such as Regional Hydro-Ecologic Simulation System (RHESSys) aim to link hydrology with ecology to model the movements water, carbon and nutrients together (Tague et al., 2004). These complex models are difficult because of the number of variables and all of their potential interactions, but these are the models that are needed to predict how contaminants move in the environment (Li et al., 2017) and how the Critical Zone will respond to climate change.

Models are not perfect and are rarely 100% accurate. George E. P. Box, a world-renowned British statistician once wrote, “essentially, all models are wrong, but some are useful”. Many things can go wrong with models. Sometimes, their underlying assumptions are incorrect. Variables once thought to be not important can be the most dominant variable in reality. Variables and parameters used to develop the model can be incorrect. For these reasons, it is important to continue to fine-tune models and never rely on one simulation. For example, the Intergovernmental Panel on Climate Change (IPCC) uses dozens of models and thousands of simulations conducted by super computers to estimate how climate change will affect Earth (Solomon et al 2007).  There will always be uncertainties with applying model simulations to real life, no one can see the future. But despite their limitations, models will be our best tool to predict it.

As the Critical Zone Observatories continue to make their measurements, scientists across the network are working to build the future models that link seemingly separate process. Although we like to think of trees, rainfall, bedrock, and streams as distinct systems, they all interact and it is up to use to figure out how and why, so we can quantify how much so we can explore the past and predict the future.

Leave us a comment below where should the boundary be or if there should even be a boundary for the Critical Zone!

Have any questions about the Critical Zone? Send them our way at Askcriticalzone@gmail.com.

Science on!

Justin Richardson
Critical Zone Observatory Postdoctoral Fellow

References:

Kothyari, B.P., Verma, P.K., Joshi, B.K. and Kothyari, U.C., (2004). Rainfall–runoff-soil and nutrient loss relationships for plot size areas of Bhetagad watershed in Central Himalaya, India. Journal of hydrology, 293:137-150.

Li, L., Maher, K., Navarre-Sitchler, A., Druhan, J., Meile, C., Lawrence, C., Moore, J., Perdrial, J., Sullivan, P., Thompson, A. Jin, L., Bolton E.W., Brantley S.L., Dietrich W.E., Mayer K.U., Steefel C.I., Valocchi A., Zachara J., Kocar B., Mcintosh J., Tutolo B.M., Kumar M., Sonnenthal E., Bao C., Beisman J. (2017) Expanding the role of reactive transport models in critical zone processes. Earth-Science Reviews, 165:280-301.

Parolari, A.J., M.L. Mobley, A.R. Bacon, G.G. Katul, D.deB. Richter, and A. Porporato (2017) Boom and bust carbon-nitrogen dynamics during reforestation. Ecological Modelling 360: 108-119

Solomon, S., D. Qin, M. Manning, Z. Chen, M. Marquis, K.B. Averyt, M. Tignor and H.L. (2007) Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Miller (eds.) Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.

Tague, C.L. and Band, L.E., 2004. RHESSys: Regional Hydro-Ecologic Simulation System—An object-oriented approach to spatially distributed modeling of carbon, water, and nutrient cycling. Earth Interactions 8:1-42.

Tucker, G.E., Lancaster, S.T., Gasparini, N.M., and Bras, R.L. (2001a) The Channel-Hillslope Integrated Landscape Development (CHILD) Model, in Landscape Erosion and Evolution Modeling, edited by R.S. Harmon and W.W. Doe III, Kluwer Academic/Plenum Publishers, pp. 349-388.